Maths
What is fluency and how is it developed in our classrooms?
This is a question that can be and has been answered many different ways. Often, we find ourselves solely looking at speed and the speed at which our pupils can recall simple key number facts as the definition of fluency.
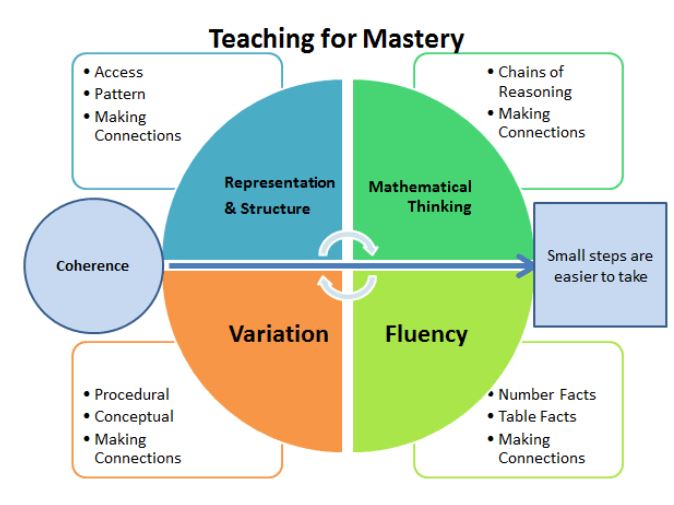
If you look at this diagram of the five principles of Mathematics, you can see why our practice sometimes leans towards this. However, the diagram not only outlines the key principles, it also shows how they are interlinked and should be revolving. These principles also ask us to teach our pupils how to make connections. This appears in all 4 areas and is, in my opinion, a key part of creating confident, enthusiastic and skilled young mathematicians.
Fluency demands more of students than memorisation of a single procedure or collection of facts. It encompasses a mixture of efficiency, accuracy and flexibility.
Quick and efficient recall of facts and procedures is important in order for students to keep track of sub-problems, think strategically and solve problems after pupils have been equipped with these skills, they must see how to use it effectively within their own problem solving and mathematical thinking.
Fluency requires the flexibility to move between different contexts and representations of mathematics, to recognise relationships and make connections, and to make appropriate choices from a whole toolkit of methods, strategies and approaches.
This seems like a long list of demands that can be overwhelming when looking at our teaching of mathematics. But as we do with the teaching of Mastery we can start with our own small steps towards best practice.
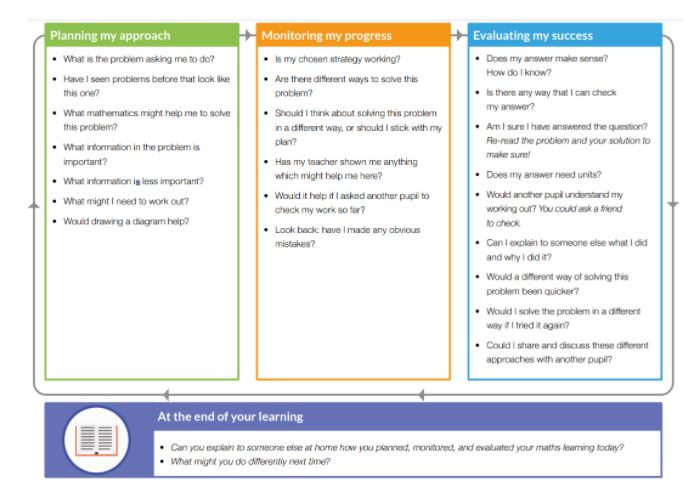
One effective strategy outlined by the EEF is, as teachers and support staff, modelling our mathematical thinking out loud. This is something many of us do already and is nothing new, but I wonder how often we deliberately plan it into our practice? The EEF have created a guidance report for improving mathematics in KS2 and KS3 from which the following resource can be found:
On the surface, this resource highlights a think aloud as a "one off" or more infrequent lesson, but there are many ways to use this resource. Personally, I see it as a list of prompts and questions first to be used by the teacher or support staff. This will then be echoed around the classroom as the pupils absorb the modelling and develop it into their own toolkits.
In their guidance report the EEF also states: Teach pupils to interrogate and use their existing mathematical knowledge to solve problems. Pupils should be encouraged to search their knowledge of similar problems they have encountered for strategies that were successful, and for facts and concepts that might be relevant.
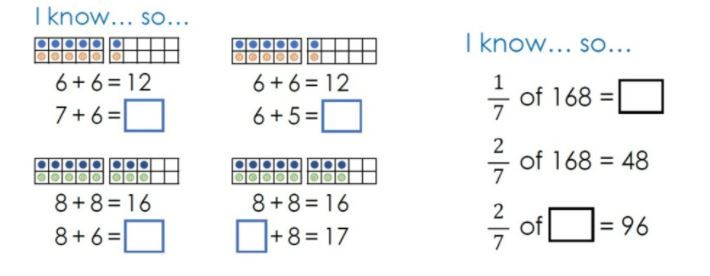
This is where we can begin to look at variation and modelling to support our development of fluency. Gareth Metcalfe has written several blog posts on the five principles of mastery and the following article supports the EEF's statement with a simple but brilliant method of questioning:
https://garethmetcalfe.wordpress.com/2018/04/02/promoting-reasoning-part-3-variation/
The "I know... so..." question is perfect for weaving links between knowledge previously taught and further links in a pupils learning alongside effective modelling. It can also lend itself to the previously mentioned "Thinking Aloud" approach.
I hope this has been useful to some, and I would love to hear if anyone else has any ideas to solve the problem of how best to develop fluency or any other of the five principles of mastery.
Henry Huxtable, Chair of Maths Lead